Final Conclusions

1. The QM/MM model of Mandelate Racemase studied in chapter 2 is able to explain the experimental reactivity trends for the three different substrates.
2. However from this QM/MM study some problems need to be clarified: We need an accurate and efficient optimizer to locate saddle points. An enzymatic study is not complete until we include the temperature effects to collect the ensemble of parallel reaction pathways in one single thermodynamic magnitude
3. The QM gas phase study in a Mandelate Racemase model is problematic due to the inherent flexibility of the active site.
4. To solve the problem of the location of stationary points in Mandelate Racemase enzyme we designed, implemented and tested the second order RFO method which optimizes minima and TS structures on QM/MM surfaces. RFO does not need the full expensive inversion of a Hessian and it has an implicit step length determination.
5. The combination of RFO with a cheap minimizer such as L-BFGS in the micro-iterative scheme is a good method to locate stationary points in big systems.
6. Some features in the micro-iterative method such as the size of the core and environment, the frequency of alternating the optimization processes in the core and in the environment and finally the interaction between the two regions has to be carefully calibrated in order to improve the micro-iterative method.
7. In the micro-iterative method there exist a core size which is a compromise between computational cost and efficiency in the search. This optimal core size will depend in particular on the number of atoms involved in the reaction step under study.
8. The 1SCF/MM method is a very good strategy to obtain the same results as full-SCF-QM/MM but with a cheaper computational cost. The 1SCF/MM method will be very useful when the QM level is expensive or many micro-iterations are required.
9. We show that an accurate TS location is always recommended. It prevents from wrong conclusions about the mechanism when the TS structure is located with a rough method such as the coordinate scan.
10. We include a section where a method to avoid the storage of very big Hessians is tested. Unfortunately the method fails in the convergence of the iterative diagonalization of the Augmented Hessian matrix. The problems may be due to the non-sparsity of a Cartesian coordinate Hessian and the possible linear dependency of the AH matrix.
11. The calculations of the potential of mean force for the Mandelate Racemase reaction permits to obtain the free energy profile. From the previous location of TS we concluded that the central step of the reaction is a double proton transfer coupled to a configuration inversion of the 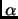$\alpha$ carbon. This makes that the geometrical reaction coordinate for the PMF calculation is not obvious.
12. A combination of four interatomic distances is the only reaction coordinate that permits to sample rather smoothly all the regions of the racemization reaction path.
13. As a conclusion of the conclusions the main thesis of this thesis is that the previous exploration of the PES of an enzymatic system is a very recommended task before a free energy computation is performed, for its low computational cost and its valuable insight into the reaction pathways.
14. However we cannot conclude without looking to the future. An improvement on the quality of the PES for enzymatic systems would permit us to move from qualitative to predictive results. Moreover, the PMF calculations still have an extreme dependence on the too short phase space exploration carried out by MD simulations and on the uncertainty involved in the a priori choice of a reaction coordinate.