



Next: Second derivative methods
Up: Introduction: Optimization Methods
Previous: Non derivative methods
Contents
First derivatives methods
The methods that require up to first derivatives of the energy with respect to the nuclear coordinates
are mainly the steepest descent and the conjugate gradient family methods [12].
Since the magnitude of the gradient indicates the steepness of the local slope,
the energy of the system can be lowered by moving each atom in response to the force acting on it.
This is the basis of the steepest descent, where the displacement of the geometry at iteration k
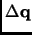 may be obtained from the gradient
may be obtained from the gradient 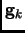 at the current geometry
at the current geometry
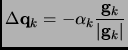 |
(2.71) |
Where 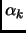 is the step length determined by trust radius or line search.
is the step length determined by trust radius or line search.
In conjugate gradient method the displacement is computed from the gradient at the current point
plus the scaled previous displacement
![$\displaystyle \Delta q_k = \alpha_k \bigl[-\frac{{\bf g}_k}{\vert{\bf g}_k\vert} + \gamma_k\Delta q_{k-1} \bigr]$](img244.png) |
(2.72) |
where the scaling factor 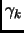 is computed using the previous gradient vectors.
There are several expressions for this factor, the easiest form is the Fletcher-Reeves
is computed using the previous gradient vectors.
There are several expressions for this factor, the easiest form is the Fletcher-Reeves
 |
(2.73) |




Next: Second derivative methods
Up: Introduction: Optimization Methods
Previous: Non derivative methods
Contents
Xavier Prat Resina
2004-09-09
![]() may be obtained from the gradient
may be obtained from the gradient ![]() at the current geometry
at the current geometry
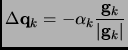
![$\displaystyle \Delta q_k = \alpha_k \bigl[-\frac{{\bf g}_k}{\vert{\bf g}_k\vert} + \gamma_k\Delta q_{k-1} \bigr]$](img244.png)
