



Next: Rational Function Optimization
Up: Second derivative methods
Previous: Second derivative methods
Contents
Newton Raphson and quasi-Newton methods
The simplest second derivative method is Newton-Raphson (NR). In a system involving N degrees of
freedom a quadratic Taylor expansion of the potential energy about the point 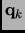 is made, where
the subscript
is made, where
the subscript 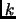 stands for the step number along the optimization.
stands for the step number along the optimization.
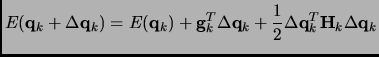 |
(2.74) |
The vector
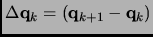 describes the displacement from the reference geometry
describes the displacement from the reference geometry 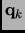 to the desired new geometry
to the desired new geometry
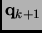 ,
,
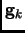 is the first derivative vector (gradient) at the point
is the first derivative vector (gradient) at the point 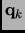 and
and 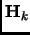 is the second derivative matrix (Hessian) at the same geometry.
Under the approximation of a purely quadratic
PES, and imposing the condition
of a stationary point
is the second derivative matrix (Hessian) at the same geometry.
Under the approximation of a purely quadratic
PES, and imposing the condition
of a stationary point
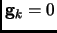 we have the Newton-Raphson equation that predicts
the displacement that has to be performed to reach the stationary point.
we have the Newton-Raphson equation that predicts
the displacement that has to be performed to reach the stationary point.
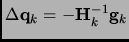 |
(2.75) |
Because the real PES are not quadratic, in practice an iterative process has to be done to reach the stationary point, and
several steps will be required. In this case the Hessian should be calculated at every
step which is high computationally demanding. A variation on the Newton-Raphson method
is the family of quasi-Newton-Raphson methods (qNR), where an approximated Hessian matrix 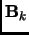 (or its inverse) is gradually updated using the gradient and displacement vectors of the previous steps.
In section 1.3.4.4 we will summarize these methods to update the Hessian.
(or its inverse) is gradually updated using the gradient and displacement vectors of the previous steps.
In section 1.3.4.4 we will summarize these methods to update the Hessian.




Next: Rational Function Optimization
Up: Second derivative methods
Previous: Second derivative methods
Contents
Xavier Prat Resina
2004-09-09
![]() is made, where
the subscript
is made, where
the subscript ![]() stands for the step number along the optimization.
stands for the step number along the optimization.