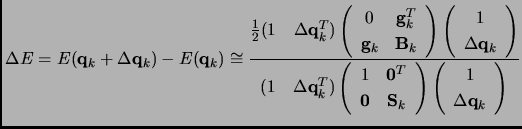Next: Direct Inversion of Iterative
Up: Second derivative methods
Previous: Newton Raphson and quasi-Newton
Contents
Rational Function Optimization
While standard Newton-Raphson is based on the optimization on a quadratic model, by
replacing this quadratic model by a rational function approximation we obtain the RFO
method [130,131].2.6
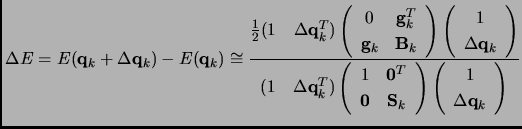 |
(2.76) |
The numerator in equation 1.76 is the quadratic model of equation 1.74.
The matrix in this numerator is the so called Augmented Hessian (AH). 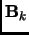 is the
Hessian (analytic or approximated). The
is the
Hessian (analytic or approximated). The 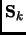 matrix is a symmetric matrix that has to
be specified but normally is taken as the unit matrix
matrix is a symmetric matrix that has to
be specified but normally is taken as the unit matrix 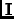 .
The solution of RFO equation, that is, the displacement vector
.
The solution of RFO equation, that is, the displacement vector
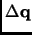 that extremalizes
that extremalizes 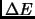 (i.e.
(i.e.
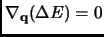 )
is obtained by diagonalization of the Augmented Hessian matrix
solving the
)
is obtained by diagonalization of the Augmented Hessian matrix
solving the 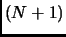 -dimensional eigenvalue equation 1.77
-dimensional eigenvalue equation 1.77
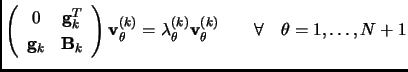 |
(2.77) |
and then the displacement vector
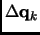 for the
for the 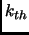 step is evaluated as
step is evaluated as
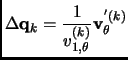 |
(2.78) |
where
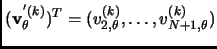 |
(2.79) |
In equation 1.79, if one is interested in locating a minimum then 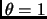 ,
and for a transition structure
,
and for a transition structure 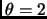 . As the optimization process converges,
. As the optimization process converges,
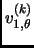 tends to 1 and
tends to 1 and
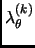 to 0.
to 0.




Next: Direct Inversion of Iterative
Up: Second derivative methods
Previous: Newton Raphson and quasi-Newton
Contents
Xavier Prat Resina
2004-09-09