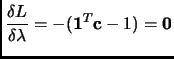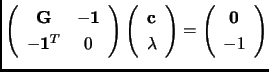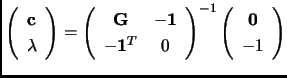Next: Update expressions and initial
Up: Second derivative methods
Previous: Rational Function Optimization
Contents
Direct Inversion of Iterative Space (DIIS)
The DIIS method [132] was firstly applied to SCF convergence problems and then
addressed to geometry optimizations [133].
The method is suitable at the vicinity of the stationary point, and it
is based on a linear interpolation/extrapolation of the available structures so as to minimize
the length of an error vector.
The DIIS method minimizing the gradient (GDIIS) has been implemented in section 3.1 in the RFO framework,
therefore it will be briefly described.
We want to obtain a corrected gradient
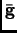 as a combination of the previous
as a combination of the previous 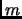 gradient vectors
gradient vectors
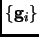
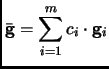 |
(2.80) |
The error function to minimize is
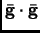 with the condition
with the condition
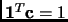
Then, building the corresponding Lagrangian in the matrix form
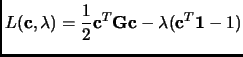 |
(2.81) |
Where
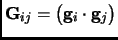 is the matrix containing the scalar products between
the gradients of the last
is the matrix containing the scalar products between
the gradients of the last 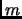 steps.
steps. 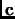 is the coefficient vector containing as much components
as iterations. The dimension of matrix
is the coefficient vector containing as much components
as iterations. The dimension of matrix 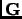 and vector
and vector 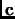 is equal to the number of iterations.
Derivating 1.81 with respect to
is equal to the number of iterations.
Derivating 1.81 with respect to 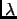 and to
and to 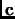 and imposing the stationary condition
and imposing the stationary condition
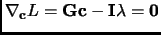 |
(2.82) |
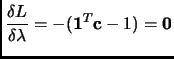 |
(2.83) |
Joining both derivative conditions in matrix form
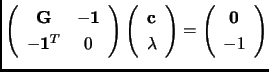 |
(2.84) |
and then
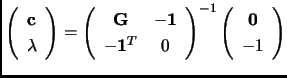 |
(2.85) |
To obtain the coefficients 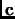 only requires the inversion of a matrix as large as the number of iterations + 1.
From the previous system of equations we can have the improved gradient
and then build up the improved Augmented Hessian
only requires the inversion of a matrix as large as the number of iterations + 1.
From the previous system of equations we can have the improved gradient
and then build up the improved Augmented Hessian
 |
(2.86) |




Next: Update expressions and initial
Up: Second derivative methods
Previous: Rational Function Optimization
Contents
Xavier Prat Resina
2004-09-09
![]() as a combination of the previous
as a combination of the previous ![]() gradient vectors
gradient vectors
![]()
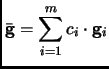
![]() with the condition
with the condition
![]()