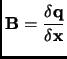Cartesian, internal and redundant coordinates

It is well known that in any optimization problem, the choice of coordinates can have an important influence on the efficiency of the optimization. Cartesian coordinates are easy to define and are used for calculating the molecular energy and its derivatives. However, the potential energy surface has very strong coupling between coordinates when represented in Cartesians.

On the other hand internal coordinates (bond lengths, valence angles and torsions) are more appropriate coordinates to describe the behavior of molecules. Because they express the natural connectivity of chemical structures, there is much less coupling between these internal coordinates.

There are different types of redundant internal coordinate systems (primitive, natural, delocalized) [149,150], and all work better than Cartesians or non-redundant internals (e.g. Z-matrix coordinates).

The transformation of Cartesian coordinates and displacements to internals is straightforward, but the transformation of the gradients requires a generalized inverse of the transformation Wilson B matrix [23]

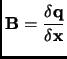$${\bf B = \frac{\delta {\bf q}}{\delta {\bf x}}}$$ (2.91)

$${\bf q = B\cdot x,\quad g}_q = {\bf B}^{-1}\cdot {\bf g}_x,\quad ... ... {\bf B}^{-T} ({\bf H}_x - \delta {\bf B}/\delta {\bf x\cdot g}_q) {\bf B}^{-1}$$ (2.92)

where x are the Cartesian coordinates, q are the (redundant) internal coordinates. See reference [149] for the meaning of ${\bf B}^{-T}$ matrix and the derivatives of ${\bf B}$. Here, we will only mention that because of the redundancy and the curvilinear nature of the internal coordinates, the transformation back to Cartesians involves an iterative process as well as a generalized inverse [149].

The calculation of a generalized inverse scales cubically. For small molecules, this is not a problem. However, for larger systems these transformations can become a bottleneck.

It has been suggested that a good initial Hessian in a second derivative optimization can decrease the coupling in Cartesian coordinates and obtain a convergence as fast as in redundant coordinates [151,2].