Second order methods for large systems

The first derivatives methods such as steepest descent and conjugate gradients are widely used to minimize molecular structures of thousands of atoms. However most of times the potential energy that describes these big systems is cheap. It means that the computational bottleneck is the storage of big matrices rather than the potential energy evaluation and its first derivative. Conversely, when potential energy is not that cheap we need the efficiency of a second derivatives method in order to save as many energy evaluations as possible. Moreover, when we are looking for transition state structures the information of the PES curvature provided by the Hessian matrix is essential for the success of the search.

Although some chain methods described in the last section are specially designed to be applied on large systems they are not able to locate stationary points by a free search. In addition, none of the chain methods uses either approximate or exact second derivatives^2.8.

The four principal strategies described in this section are optimizers that, in some extent, uses the information of the second derivatives to increase the efficiency or to keep track of the PES curvature. Avoiding at the same time the computational cost that the classical Newton-like methods usually require.

When trying to apply Newton-like methods to systems bigger than very few hundreds of atoms with the nowadays computers some computational problems arise. Three main bottle-necks exist

• Computation of an accurate initial Hessian scales with 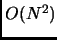$O(N^2)$ when calculated numerically
• Diagonalization process that scales with $O(N^3)$
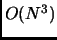
• Hessian storage scales with $O(N^2)$
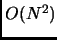
• Internal-Cartesian coordinates interconversion scales with $O(N^3)$

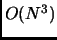
The scaling factor must not be directly related to the computational cost. These four problems appear at different size and situations (see section 3.4 for a particular benchmark). For example depending on the level of theory of the energy, the second derivatives calculation can be the main computational demanding task. A full diagonalization will be problematic when both the system has hundreds of dimensions and the process must be performed at every step of a long optimization. The storage will not be a problem until the system has about tens of thousand atoms^2.9Finally, the internal-Cartesian coordinates interconversion scales as the diagonalization but in this thesis only Cartesian coordinates will be used.