| (2.94) |
The adopted basis Newton-Raphson method (ABNR) was developed originally by M. Karplus and D.J. States. It has been used widely for the optimization of biomolecules since its original implementation in CHARMM package [53]. Even though, there has never been a paper describing the method and the corresponding implementation. Only in a very recent paper by B. R. Brooks and co-workers [144] we can find some equations that picture the most important aspects of the method.
In the ABNR minimization the Newton-Raphson scheme is only applied in a small subspace of the molecule. So the whole displacement of the geometry is a combination of a steepest descent(SD) step plus a small contribution of Newton-Raphson(NR).
| (2.94) |
At the beginning of the minimization only the steepest descent component is employed (
![]() ).
After several SD steps, the last
).
After several SD steps, the last ![]() geometry displacements can be used as a basis
geometry displacements can be used as a basis
![]() of dimension
of dimension
![]() to obtain the NR step. So at step
to obtain the NR step. So at step ![]() the last
the last ![]() geometries are used
geometries are used
![]()
 |
(2.95) |
This equation can be approximated in a Taylor expansion with respect
to ![]() and then the Newton-Raphson equation becomes
and then the Newton-Raphson equation becomes
Equation 1.96 is a set of ![]() equations that can be solved diagonalizing the small
equations that can be solved diagonalizing the small ![]() matrix.
With the coefficients
matrix.
With the coefficients
![]() we can obtain the geometry displacement component
we can obtain the geometry displacement component
![]() .
But what incorporates the Hessian character in ABNR method is the particular steepest descent step that is computed in
the following way
.
But what incorporates the Hessian character in ABNR method is the particular steepest descent step that is computed in
the following way
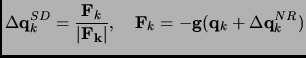 |
(2.97) |
![$\displaystyle {\bf g}({\bf q}_j+\Delta {\bf q}_k^{NR})\approx {\bf g}({\bf q}_k)+\sum_{l=1}^m [{\bf g}({\bf q}_{k-l})-{\bf g}({\bf q}_{k})]c_{lk}$](img321.png) |
(2.98) |