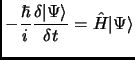Basic equations for a molecular system

The equations that rule a non-relativistic and unperturbed molecule are given by the Quantum Mechanics formulation.

From the fifth postulate in atomic units we have the time dependent Schrödinger equation that describes the evolution of a quantum system.

$$-\frac{\hbar}{i}\frac{\delta \vert\Psi\rangle}{\delta t}=\hat H \vert\Psi\rangle$$ (2.1)

Where $\vert\Psi\rangle$ is the vector of the space that contains all the information of the system and $\hat H$ is the Hamiltonian operator (the sum of kinetic and potential energy). Under the representation of positions the vector becomes the wave function and for a molecular system this Hamiltonian has the following form

$$\hat H=\hat T_N+\hat T_e+\hat V_{NN}+\hat V_{Ne}+\hat V_{ee}$$ (2.2)

or in a more detailed description

$$\hat H = -\frac{1}{2}\sum_K^{\tiny nuclei}\frac{\Delta_K}{m_K} -\frac{1}{2... ...ny electrons}\Delta_i +\sum_K^{nuclei}\sum_{K>L}^{nuclei}\frac{Z_K Z_L}{R_{KL}}$$

$$-\sum_i^{electrons}\sum_K^{nuclei}\frac{Z_K}{r_{iK}} +\sum_i^{electrons}\sum_{i>j}^{electrons}\frac{1}{r_{ij}}$$ (2.3)

Under the consideration that $\vert\Psi\rangle$ is a stationary state we get the time independent Schrödinger equation

$$\hat H\vert\Psi\rangle = E \vert\Psi\rangle$$ (2.4)

The value $E$ is the energy eigenvalue of the Hamiltonian operator, a scalar that offers the spectrum of the operator.

The equation 1.4 cannot be solved exactly for a molecular system. The term $\hat V_{Ne}$ in equation 1.2 does not permit to solve the independent Schrödinger equation by splitting the problem into a nuclear part separated from an electronic part. Consequently we will need to solve the equation 1.4 by different stages. This two-stage solution is provided by the Born-Oppenheimer approximation.