Empirical observations of molecular spectroscopy show that the total energy of a molecule can be viewed as the sum of several approximately non-interacting parts. Born-Oppenheimer approximation shows how the electronic motions can be approximately separated from the nuclear motions.
Let us define a molecule by a geometry structure determined by the nuclear positions.
If the nuclei have fixed positions,
the nuclear kinetic term vanishes
![]() and the nuclear repulsion term
and the nuclear repulsion term
![]() becomes a constant.
The Hamiltonian expression of equation 1.2 has a shortened form that we label as electronic Hamiltonian
becomes a constant.
The Hamiltonian expression of equation 1.2 has a shortened form that we label as electronic Hamiltonian
The solutions of the electronic Hamiltonian are the electronic wavefunctions that will
have to be solved for every nuclear configuration ![]()
The solutions {
![]() } is a complete set of functions of the n-electrons space.
So, the total wavefunction of the system should belong to a full space
created from the tensorial product between the nuclear space and electronic space:
} is a complete set of functions of the n-electrons space.
So, the total wavefunction of the system should belong to a full space
created from the tensorial product between the nuclear space and electronic space:
![]() .
.
Although it is not a basis of the whole space, in the Born-Oppenheimer expansion the crossed terms are avoided and the wavefunction has the form
If the total wavefunction has the form of equation 1.9 when it is introduced in the total Schrödinger equation 1.4 we have
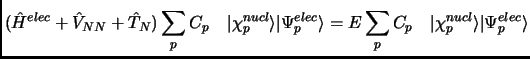 |
(2.10) |
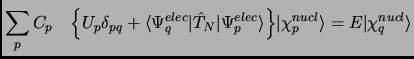 |
(2.11) |
| (2.12) |
| (2.14) |
In conclusion, the nuclei move on a Potential Energy Surface (PES) ![]() ,
where
,
where ![]() comes from the solution of electronic Schrödinger
equation 1.6, and
comes from the solution of electronic Schrödinger
equation 1.6, and ![]() is the total energy of the system.
The PES is a concept that will be used all along this thesis and we must keep in mind the level of approximations
we have assumed to achieve such concept.
is the total energy of the system.
The PES is a concept that will be used all along this thesis and we must keep in mind the level of approximations
we have assumed to achieve such concept.