Long range interactions

When size increases the most time-consuming process is the computation of non-bonded interactions shown in equation 1.57 and 1.58. For a pairwise model the number of non-bonded evaluations increase as the square of the number of atoms. However sometimes such computational effort is not necessary, for example, the van der Waals interactions reproduced by a Lennard-Jones potential decays very rapidly (at a distance of 2.5$\sigma$ there is only 1% of the interaction at $\sigma$).

Non-bonded cutoff:
A very popular strategy is to set a cutoff distance. In this method each atom or group of atoms interacts with all the atoms that are closer than the considered cutoff. The rest of the atoms that fall outside this sphere of interaction do not contribute to the energy nor the gradient of the considered atom. It has been seen that the simple truncation can be too rough, actually in this case the energy is not conserved. Sometimes a cubic switching function is used at a certain distance in order to obtain a smooth decay. At a certain distance $r_{on}$ the switching function is activated so that the potential is reduced until it vanishes at distance $r_{off}$. For the switch approximation the following $S(r)$ function is multiplied to the potential energy

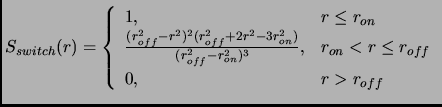$$S_{switch}(r) = \left\{ \begin{array}{ll} 1, & r \leq r_{on} \\ ... ...r_{on}^2 )^3 }, & r_{on}<r\leq r_{off} \\ 0, & r > r_{off} \end{array} \right.$$ (2.60)

As an alternative, the whole interaction can be shifted and smoothed to avoid the abrupt truncation[48]. In this case the $S(r)$ function has the following expression

$$S_{shift}(r) = \left\{ \begin{array}{ll} (1-(r/r_{off})^2)^2, & r \leq r_{on} \\ 0, & r > r_{off} \end{array} \right.$$ (2.61)

See figure 1.2 for an approximated shape of the cutoff potentials.

Figure 1.2: Potential energy profile corresponding to the different cutoff approximations

Related to the non-bonded cutoff strategy, an additional problem arises. We must compute all the distances between each atom to decide whether its contribution is calculated or not, that is, every atom has a list of the nearest interacting atoms. If we had to calculate this list at every step of a Molecular Dynamics run it would be too expensive. So this non-bonded pair-list is built atom-wise or group-wise and it is updated every certain frequency.

We have seen that there are many parameters that we have to consider. A cutoff distance for the electrostatics and for the van der Waals, a cutoff for the smooth decay, a frequency for the non-bonded pair-list update. Despite of all these variables some experience on these kind of simulations has been accumulated, and the different possibilities and the extent of the error has been reported [48,49].

Minimum image and periodic boundary:
The simulations in condensed phase usually have to reproduce an infinite bulk system such as the solvent that surrounds our solute. If this solvent is reproduced by a single box of solvent the edge of the box will have an artificial surface tension. In this case the Periodic Boundary Conditions is the most suitable strategy. The box is reproduced throughout the space to form an infinite lattice. In the course of a simulation, as a molecule moves in the original box, each periodic image in the neighboring boxes moves in exactly the same way.

Obviously all the possible interactions in an infinite lattice would be infinite. An adequate approximation is the minimum image convention where every atom in the original box interacts with the nearest elements that fall within the given cutoff. These interacting atoms may be in the original box or in the neighboring, however, in order to avoid the interaction of a molecule with itself the cutoff must be smaller than the half of the box.

Long range electrostatic effects:
We may find the truncation schemes described above a brute-force strategy. Mainly for electrostatics there are cases where the interaction does not decay that fast and the cutoff approximation is not adequate. The Ewald lattice-sum, Fast Multipole Method (FMM) and the Reaction Field approximations are the possible solutions [50]. These methods are appropriate for highly charged systems and for the calculations of some delicate magnitudes such as the dielectric constant. Even though, the Ewald summation, which calculates the true electrostatic interactions for an infinitely repeating system, imposes long-range correlations on the system that may be undesirable, and it is computationally more expensive than spherical-cutoff methods.