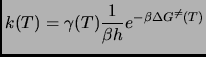 |
(2.129) |
i) Reactant states are in local equilibrium along a progress coordinate, which is the reaction coordinate.
ii) Trajectories that cross the transition state hypersurface
do not recross it before becoming thermalized on the reactant or product side
iii) The reaction coordinate degree of freedom can be separated from the rest and it is treated by classical mechanics.
The rate constant at a given temperature T is
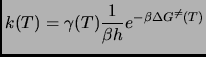 |
(2.129) |
| (2.130) |
For a review of the current status of the TST theory see reference [203], and [62] for TST applied to enzymatic systems.
However, the most expensive and problematic task is the computation of the free energy difference
![]() , which
must be calculated along a predefined reaction coordinate. In some condensed phase reactions the mechanism should be intuitively
predicted, such as proton transfers, and therefore the reaction coordinate is adequately chosen.
On the other hand, many
other reactions have a complicated or unpredictable mechanism and therefore the choice of a predefined reaction coordinate is difficult.
A paradigmatic example is the reaction of autoionization of water [204].
In this sense there has been recent improvements in the computation of reaction rates
without the knowledge of the reaction mechanism through transition path sampling method [137],
but the computational cost is still too high and some alternatives are needed to model enzymatic reactions adequately.
, which
must be calculated along a predefined reaction coordinate. In some condensed phase reactions the mechanism should be intuitively
predicted, such as proton transfers, and therefore the reaction coordinate is adequately chosen.
On the other hand, many
other reactions have a complicated or unpredictable mechanism and therefore the choice of a predefined reaction coordinate is difficult.
A paradigmatic example is the reaction of autoionization of water [204].
In this sense there has been recent improvements in the computation of reaction rates
without the knowledge of the reaction mechanism through transition path sampling method [137],
but the computational cost is still too high and some alternatives are needed to model enzymatic reactions adequately.