First of all only the valence electrons are considered explicitly, that is, there will be only basis functions for them, so the nucleus in the electronic Hamiltonian will have a lowered effective charge
Only valence electrons with minimal basis set:
First of all only the valence electrons are considered explicitly, that is, there will be only basis
functions for them, so the nucleus in the electronic Hamiltonian will have a lowered effective charge ![]() due to the screening by the core-electrons2.2.
Moreover, the basis set used for the valence electrons will be minimal. It means, for example, one
function for hydrogen and four functions, representing the s and three p, for the second and third
row elements.
due to the screening by the core-electrons2.2.
Moreover, the basis set used for the valence electrons will be minimal. It means, for example, one
function for hydrogen and four functions, representing the s and three p, for the second and third
row elements.
Discarding integrals: ZDO approximation
Most of the semiempirical strategies are based on the Zero Differential Overlap approximation (ZDO).
That is to consider zero the product (not the integral) between two basis functions.
| (2.36) |
In particular, the Neglect of Diatomic Differential Overlap (NDDO) method sets
to zero only those products which functions are centered on different atoms ![]() and
and ![]() that depend on the same electron coordinates.
that depend on the same electron coordinates.
| (2.37) |
![$\displaystyle F_{\mu\nu}=h_{\mu\nu} + \sum_{\lambda,\sigma}^{AO} P_{\lambda\sig...
...langle\mu\nu\vert\lambda\sigma\rangle - \langle\mu\lambda\vert\nu\sigma\rangle]$](img138.png) |
(2.38) |
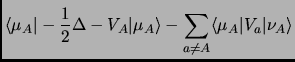 |
(2.39) | ||
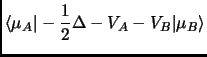 |
(2.40) |
| (2.41) |
Since many terms are discarded the rest of integrals must be parameterized by experimental data, in such a way that we include in the surviving terms a correction to give the adequate results.
Further approximated methods exist, for example, the Completely Neglect Differential Overlap (CNDO) and the Intermediate Neglect Differential Overlap (INDO) Hamiltonians, which discard even more elements of the Fock matrix. Although these methods had their importance in the sixties and seventies they are not used any more. The methods currently used and still improved such as the Modified Neglect of Diatomic Overlap (MNDO) [30], the Austin Model 1 (AM1) [31] and the Parameterized Model 3 (PM3) [32,33] are based on the NDDO Hamiltonian. They only differ in the way the core-core repulsion is treated and how the atomic parameters are assigned. There are other new methods such as MNDO/d, SAM1, ZINDO and PM52.3. We will not comment the differences between these methods, check the reference [34] for an updated review in semiempirical methods.
Some earlier versions of semiempirical approximations prior to the ZDO-type existed for the treatment of the ![]() -bonds.
The Hückel method, the Pariser-Parr-Pople are some examples of such over simplification.
However no useful results for the molecular structure came out until the explicit treatment of
-bonds.
The Hückel method, the Pariser-Parr-Pople are some examples of such over simplification.
However no useful results for the molecular structure came out until the explicit treatment of ![]() -bond
with Pople's CNDO [35].
-bond
with Pople's CNDO [35].
The most frequently used Hamiltonians in QM/MM enzymatic studies are AM1 and PM3. Both of them have their own recognized failures. A clear example is the low rotation barrier in amide bond which is usually corrected by an additional molecular mechanics term. Another required improvement is the adequate description of hydrogen bonds [36]. While AM1 has been parameterized by hand in a chemical intuition fashion, PM3 parameters have been obtained in a relatively automated way using a wider range of chemical data. However its accuracy is very similar, so before the choice a previous comparison with ab initio results is always recommended.