The application of the DFT to the computational chemistry was not found useful until the late eighties. After that time, the DFT techniques have had an explosion of successful applications to chemical problems due to the usage of more appropriate functionals for these kind of systems [38,39].
The DFT applied to a molecular system may be solved in such a way that keeps many parallelism with the already explained Hartree-Fock wave mechanics. However, in this case the electron density distribution plays a central role rather than the many-electron wavefunction. In defense of the DFT it is said that while in some cases the wave mechanics must take into account thousands of determinants into the wavefunction, the DFT gives an easier understanding by its only three-space coordinates electron density.
Kohn-Sham equations:
The equivalent of
the Hartree-Fock equations in DFT are the self consistent Kohn-Sham equations (KS)[40].
Although this is not the only way to consider the DFT equations, it is the most frequently used in computational chemistry,
so we will focus on this particular aspect of the DFT, the rest of applications and theories
may be found in the literature[41].
This strategy can be seen as modeling an independent particle model that is able to reproduce, in theory,
the full interacting system.
The energy is obtained through a sum of separated
functionals of the electronic density ![]() .
.
For the kinetic term ![]() Kohn and Sham proposed to define an independent electron system
described by a set of orbitals {
Kohn and Sham proposed to define an independent electron system
described by a set of orbitals {![]() } that give a density
} that give a density ![]()
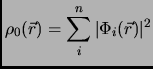 |
(2.44) |
| (2.45) |
The kinetic term corresponding to this hypothetical system ![]() , although it is not the exact, is known and is the one
that is used for HF.
, although it is not the exact, is known and is the one
that is used for HF.
![$\displaystyle T_0[\rho]=\sum_i^n \langle \Phi_i\vert-\frac{1}{2}\Delta_i\vert\Phi_i\rangle$](img158.png) |
(2.46) |
| (2.48) |
Despite of the new nomenclature it is easy to see that equation 1.47 has similar
functionality that the Hartree-Fock expression. So if the functional
![]() is only the exchange part
is only the exchange part ![]() found in the HF scheme (equation 1.26)
we recover the same HF expression.
In this sense, the implementation of HF equations might be seen as a particular case
of the DFT-KS equations.
However, if the functional
found in the HF scheme (equation 1.26)
we recover the same HF expression.
In this sense, the implementation of HF equations might be seen as a particular case
of the DFT-KS equations.
However, if the functional
![]() was known we would obtain the exact energy
including all the electron correlation.
was known we would obtain the exact energy
including all the electron correlation.
In the same manner the functional
![]() is minimized with the
constraint of the orthonormality of the Kohn-Sham orbitals. The Kohn-Sham orbitals can be spanned
as a combination of basis functions centered on every atom leading to
the Konh-Sham equations that have
the same scheme of the Roothan-Hall procedure.
is minimized with the
constraint of the orthonormality of the Kohn-Sham orbitals. The Kohn-Sham orbitals can be spanned
as a combination of basis functions centered on every atom leading to
the Konh-Sham equations that have
the same scheme of the Roothan-Hall procedure.
The computational cost of the KS equations is very similar to the Roothan-Hall-HF.
However some differences exist, it could depend strongly on the expression used for the
![]() functional.
Usually some integrals due to the exchange-correlation expression have to be evaluated numerically in a grid of points.
functional.
Usually some integrals due to the exchange-correlation expression have to be evaluated numerically in a grid of points.
![$\displaystyle \langle \phi_r\vert V_{xc}[\rho (r), \nabla\rho(r)]\vert\phi_s\ra...
..._i^{points} V_{xc}[\rho (r_i), \nabla\rho(r_i)]\phi_r(r_i)\phi_s(r_i)\Delta v_i$](img165.png) |
(2.49) |