Polarized QM/MM

The earliest hybrid method modeling the environment explicitly is the so-called combined Quantum Mechanics/Molecular Mechanics (QM/MM). In QM/MM [66,67,68] methodology a small reactive part of a chemical system is described by quantum mechanics (QM) whereas the remaining large non-reactive part is described by molecular mechanics (MM). Although the first paper is attributed to Warshel and Levitt [66] some publications make reference of a preceding work by Warshel and Karplus [69] where the electronic structure of a polyene is split in a $\pi$ system represented by a semiempirical PPP method and the $\sigma$ by an empirical force field. In any case, the method that is used today to address the reactivity of biochemical systems is still very similar to that used in 1976 by Warshel and Levitt [66]. There is a significant amount of information reviewing the current status of QM/MM methods in the literature [70,71,72,5].

Figure 1.3: QM/MM methods are based on a splitting of the system in a reactive(QM) part and an environment(MM) part

The main advantage of QM/MM methods is its easy implementation in computational codes while giving rather good chemical results. Its main disadvantage, especially in enzymatic systems, is to go beyond qualitative results and thus to obtain quantitative numbers out of QM/MM computations. This problem is mainly due to three factors: i) the need for good ab initio description for the QM part whereas the usual size of the QM part mostly only allow for semiempirical calculations; ii) the need for accessing free energy numbers through extensive sampling which is too computationally expensive; iii) the difficult calibration of the interaction between the QM part and the MM part, especially in biochemical systems as mentioned there after.

The first two factors are related to actual computational bottlenecks and should be overpassed in the near future.

Splitting the System:
In most reactive systems, the number of atoms involved in a chemical reaction is fairly limited (i.e., whose electronic properties are changed during the reaction), the rest of the atoms may have a strong influence on the reaction but this is usually limited to short and long range non-bonded interactions that can be represented through both electrostatic and van der Waals interactions. The main idea of QM/MM methodology is to split the chemical system into two parts: the first part is small and described by quantum mechanics, it is called the quantum part. The second part is the rest of the system and is described by molecular mechanics, it is called the classical part. The full Hamiltonian can therefore be expressed as:

$$\hat{H} = \hat{H}_{\mbox{\tiny QM}} + \hat{H}_{\mbox{\tiny MM}} + \hat{H}_{\mbox{\tiny QM/MM}}$$ (2.62)

where $$\hat{H}_{\mbox{\tiny QM}}$$ is the electronic Hamiltonian describing the quantum atoms in the Born-Oppenheimer approximation. It has the same expression that in equations 1.5 and 1.7 in page

In equation 1.62, the Hamiltonian $$\hat{H}_{\mbox{\tiny MM}}$$ describes the classical part. As we defined in the preceding section, a set of atoms interacting in this part can be seen as a set of point charges $\{Q_c\}$ in space interacting through a defined force field. The usual energy expression for every term of the force field has already been commented in section 1.2.2.1 (page ).

The last term $$\hat{H}_{\mbox{\tiny QM/MM}}$$ in equation 1.62 stands for the explicit interaction between the quantum and the classical part. It can be represented as the sum of two terms: a van der Waals term describing the non-electrostatic interactions between quantum and classical atoms and an electrostatic term describing the interaction between a classical point charge $\{Q_c\}$ and the electrons and nuclei of the quantum part:

$$\hat{H}_{\mbox{\tiny QM/MM}} = V_{\mbox{\tiny QM/MM}}^{\mbox{\tin... ..._K^{\mbox{\tiny nuclei}} \sum_C^{\mbox{\tiny classical}} \frac{Z_K Q_C}{R_{KC}}$$ (2.63)

Note that the second term in equation 1.63 that describes the electrons-classical charge interaction depends on the coordinates of electrons $r_{iC}$. Therefore it must be incorporated into the core Hamiltonian of the quantum subsystem and obtained through a SCF process. Indeed this term is the responsible of the polarization on the QM part due to the presence of the MM charges. The other two terms in equation 1.63 depend on particles with fixed positions and can be computed analytically as the rest of MM terms.

QM/MM interactions:
The Hamiltonian $\hat{H}_{\mbox{\tiny QM/MM}}$ should reproduce quantitatively the interaction between the QM and MM parts as if the system was computed fully quantum mechanically [73]. The quantitative reproduction of the QM/MM interactions depends on three points:

1) the choice of the set of non-polarizable point charges $\{Q_C\}$ or more generally of the MM force field;
2) the choice of the van der Waals parameters to describe $$V_{\mbox{\tiny QM/MM}}^{\mbox{\tiny van der Waals}}$$;
3) the way the classical charges polarize the quantum subsystem.

It is usually a good approximation to take the charge definition from an empirical force field and to incorporate those charges into the core Hamiltonian of the quantum subsystem, being this one the procedure used in this thesis. This gives quite reliable results because the charges in molecular mechanics are defined in order to reproduce electrostatic potential properly [74]. However, it is well-known that between different force fields the charge definition on atoms can change dramatically, even between different generations of the same force field. These differences between different set of charges should have a non-negligible impact on the quality of a QM/MM study.

The choice of van der Waals parameters is another crucial point in the production of a good QM/MM interaction. In theory, a new set of parameters should be defined for each atom in the system (QM + MM) to exclusively compute $$V_{\mbox{\tiny QM/MM}}^{\mbox{\tiny van der Waals}}$$ [75,76]. It is well known that the parameters from a forcefield are optimized in a consistent fashion. In consequence the new van der Waals parameters should be compatible with the forcefield used. In practice, one uses the van der Waals parameters from the current force field definition for each atom in the MM part and, when possible, define a new set of van der Waals parameters for the QM atoms [77,78].

A third point needing to be clarified in the description of QM/MM interactions is the way the classical set of charges $\{Q_C\}$ polarize the electronic wavefunction from the QM subsystem. This is usually done by adding to the core Hamiltonian of the QM part a perturbation describing the interaction between the QM electrons and the classical charges. An element of the core Hamiltonian matrix is expressed as:

$${h'}_{pq}^{\mbox{\tiny core}} = <\phi_p\vert\hat{h'}^{\mbox{\tiny core}}\vert\phi_q>$$

$$= h_{pq}^{\mbox{\tiny core}} - \sum_i^{\mbox{\tiny electrons}} \sum_{C}^{\mbox{\tiny classical}} <\phi_p\vert\frac{Q_C}{r_{iC}}\vert\phi_q>$$ (2.64)

However with NDDO semiempirical Hamiltonians its has been shown [75] that electron-classical charges and nuclei-classical charges interactions should not be treated in the same way as electron-nuclei and nuclei-nuclei interactions.

Cutting covalent bonds:
In the study of chemical reactions in solution with QM/MM methods the solute usually belongs to the quantum part and the solvent to the MM part, so that the two zones are perfectly differentiated. However, in enzymatic reactions the reactive part treated with QM usually includes the substrate and some residues that participate actively in the chemical reaction. In consequence, the frontier between the two zones, mainly in lateral chains of the active aminoacidic residues resides on a covalent bond.

In this case the way to link the QM and MM part is not straightforward. A problem occurs at this frontier because the electron of X (see figure above) involved in the covalent bond with Y is not paired with any other electron because in molecular mechanics the electrons of Y are not explicitly represented. This unpaired electron would give a radical character in the QM part that would change all the chemistry.

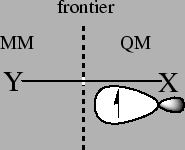
The way this frontier between the two zones is treated has been the objective of many publications. Actually, many laboratories that developed their tools in QM/MM schemes have their own method to treat the frontier

The different solutions can be divided in two main categories. Those that add an atom or pseudoatom to fill the valencies on the quantum frontier, and those which deal specifically with the frontier bond orbital by trying to compute directly its main characteristics from known parameters. In table 1.1 some of the different approaches published so far with its original references is given.

Table 1.1: A brief classification of the methods addressed to treat the covalent frontier in QM/MM methods

General Strategy	Name and Reference
914mmAdding an Atom	Link atom (blind) [68]
	Dummy groups[79]
	Link atom (partial interaction) [80,81]
	Adjusted Connection atoms [82]
	Pseudohalogens[83]
	Pseudobond approach [84]
	Double link atom [85]
	Quantum capping potentials [86]
	AddRemove [87]
414mmFrontier Bond Orbital	Proposed bonding hybrid orbital [66]
	Local SCF (LSCF) [88,89,90]
	Generalized Hybrid Orbital (GHO) [91,92,93,94]
	Frozen orbital [95]

In this thesis we have used the Link atom approximation in chapter 2 and the Generalized Hybrid Orbital (GHO) in chapter 4. The Link atom method is the simplest implemented and widest used method. It consists in adding a monovalent atom, the so-called link or dummy atom, along the X--Y bond to fill the valency of the quantum frontier atom X. Usually, this link atom is an hydrogen [68], but some implementations use an halogen like fluorine or chlorine [96]. This method has two major problems still in debate: The interaction of this link atom with the classical part and its additional degree of freedom. See reference [5] for a deeper discussion.

The GHO formalism is an extension of the LSCF method which at the same time is derived from the original work from Warshel and Levitt [66]. In GHO the classical frontier atom is described by a set of orbitals divided into two sets of auxiliary and active orbitals. The latter set is included in the SCF calculation, while the former generates an effective core potential for the frontier atom.

Figure 1.4: Schematic representation of GHO model for the QM/MM frontier

As we can see, it seems that there are many variations in QM/MM methods. These methods are still under development and there is not yet a unique and standardized procedure to be used as a black box. Actually, one must face some numerical and methodological problems for every system under study.

More accurate potentials:
Most of publications using QM/MM methods have chosen semiempirical Hamiltonians in the QM part. This is mainly because an exploration of the configuration space requires thousands of energy and gradient evaluations that so far only semiempirical methods are fast enough to be permitted. An interesting initiative is the coupling of a semiempirical DFT method (SCC-DFTB) with CHARMM package [97], which is a good compromise between accuracy and computational cost[98]. However, many groups have interfaced ab initio packages to MM programs to perform QM/MM at a higher level of accuracy. Programs such as Gaussian98, GAMESS-US, GAMESS-UK, CADPAC, HONDO, DALTON, JAGUAR, deMon, Turbomol are used to carry out Hartree-Fock/MM[99,100], DFT/MM[101,102,90,103,104], or even Coupled Cluster/MM [105].

Finally we must not forget the Carr-Parrinello approximations [106] that has been interfaced with GROMOS force field to perform ab initio simulations of biological systems[107]. Even though, as we have seen, QM/MM methods are far from being accurate. Therefore, in addition to an insufficient sampling, the frontier, the arbitrary polarization charges are sources of error in such a way that the increase of accuracy in the QM part may be in some cases wasted.