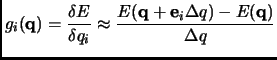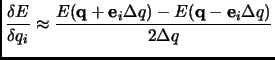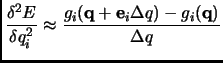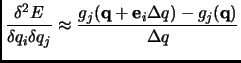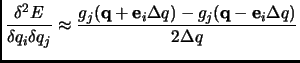Derivatives of the potential energy

The derivative of the potential energy respect to its geometrical (nuclear) coordinates is a crucial issue needed in optimization and molecular dynamics methods.

It is obvious that depending on the energy expression the derivative will be an affordable task or not. There are available methods to calculate the first, the second and sometimes higher order derivatives of the energy.

In general there are two ways to calculate the energy derivatives, numerically and analytically.

• Numerical derivatives
  Numerical derivatives will be a more expensive task but easier to implement. In this case the derivative is approximated by small finite displacements of the geometry and performing energy evaluations at the displaced structures.

  The $ith$ gradient component $g_i({\bf q})$ of a molecular system with a geometry ${\bf q}$ can be approximated as:

  $$g_i({\bf q}) = \frac{\delta E}{\delta q_i} \approx \frac{E({\bf q}+{\bf e}_i\Delta q)-E({\bf q}) }{\Delta q}$$ (2.67)

  
  
  where $ith$ coordinate has been displaced $\Delta q$. The ${\bf e}_i$ vector has zero in its components but 1 in the $ith$ component.

  An improvement to the equation 1.67 is displacing the $ith$ coordinate forward and backward. ^2.4

  $$\frac{\delta E}{\delta q_i} \approx \frac{E({\bf q}+{\bf e}_i\Delta q)-E({\bf q}-{\bf e}_i\Delta q)}{2\Delta q}$$ (2.68)

  
  

  The same argument can be used for second derivatives. In this case we have diagonal $H_{ii}$ and off-diagonal $H_{ij}$ elements of the Hessian matrix:
  

  $$H_{ii} = \frac{\delta^2 E}{\delta q_i^2} \approx \frac{g_i({\bf q}+{\bf e}_i\Delta q) - g_i({\bf q}) }{\Delta q}$$

  $$H_{ij} = \frac{\delta^2 E}{\delta q_i \delta q_j} \approx \frac{ g_j( {\bf q}+{\bf e}_i\Delta q )- g_j({\bf q})} {\Delta q}$$ (2.69)

  
  
  And with the forward-backward improvement.
  

  $$H_{ii} = \frac{\delta^2 E}{\delta q_i^2} \approx \frac{ g_i({\bf q}+{\bf e}_i\Delta q) - g_i({\bf q} - {\bf e}_i\Delta q) }{2\Delta q}$$

  $$H_{ij} = \frac{\delta^2 E}{\delta q_i \delta q_j} \approx \frac{ g_j({\bf q}+{\bf e}_i\Delta q) - g_j({\bf q} - {\bf e}_i\Delta q)}{2\Delta q}$$ (2.70)

  
  

  The quality of the derivative depends on the magnitude of $\Delta q$ and the accuracy of potential energy $E({\bf q})$. (See section 3.1.1.2 for the numerical quantities of these magnitudes and some practical recommendations to decrease the high computational cost of numerical derivatives)

• Analytical derivatives
  Analytical derivatives have a more complicated expression than the equations above. It can be found in the bibliography first and second derivatives for many of the QM methods (based on the Coupled Perturbed Hartree Fock equations [10,28] or on Hellman-Feynman theorem). There are also derivatives in Cartesian coordinates for the most common terms in a Molecular Mechanics force field. Recently Cui and Karplus published the analytical second derivatives for a QM/MM potential energy expression [127].