Initial Hessian on minimization and TS search

We tested two forms of initial Hessian matrix. The first is the identity matrix. The second is a numerical Hessian. The initial numerical Hessian matrix used in this section has the shape shown in figure 3.1

Figure 3.1: Approximated initial Hessian designed to optimize large systems

This form has been proposed in reference [155] in order to avoid the storage of a big matrix. The systems tested in this section are not that big, but we wanted to know the behavior of such initial Hessian in order to apply it to really big systems (section 3.4).

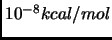The numerical Hessian components have been calculated by forward-backward expression (equation 1.70 in page ) of the gradient. We have seen that the numerical value has an important dependence on the convergence criteria in the SCF calculation and on the finite displacement of the geometry. So, after some benchmarks tests we determined the SCF threshold to $10^{-8} kcal/mol$ and the finite displacements reduced to 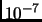$10^{-7}$Å.

We have also tested some strategies to build faster the numerical Hessian matrix:

• 1SCF/MM for MM atoms: When calculating the derivatives corresponding to MM atoms only one cycle in the SCF process is done
• pure MM for MM atoms: discard the QM and QM/MM part of the Hamiltonian for the MM atoms far away from the quantum zone.

However, we have noticed a strong dependence of the number steps required to converge on the quality of the approximated Hessian. So, hereafter QM(full SCF)/MM interaction is used for the numerical derivatives.