External minimizers: BFGS and L-BFGS

The RFO method will be compared with the quasi Newton process BFGS[12,136] method and with the limited memory L-BFGS[153].

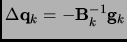$$\Delta {\bf q}_k=-{\bf B}^{-1}_k {\bf g}_k$$ (4.8)

Few comments will be devoted to these methods here. They have already been described in section 1.3. We will only point out that the BFGS implemented here starts the iterative process with the identity matrix as initial Hessian. As the optimization proceeds, an update of the inverse of the Hessian is build up following the BFGS formula (equation 3.6). So no matrix diagonalization is required and, therefore, there is no test on the suitable curvature of the surface.

The limited memory BFGS, the so-called L-BFGS procedure has also been described in section 1.3.7.1. It is important to note that the unique difference, as we have implemented here, between BFGS and LBFGS is that while the former builds the inverse of the Hessian matrix at every iteration and stores it in memory, the latter never stores the whole Hessian, but only the gradient and the position of a certain number of previous steps in order to perform on the fly, the matrix-vector product 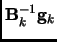${\bf B}^{-1}_k {\bf g}_k$ of equation 3.8.