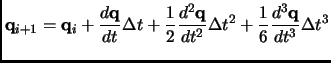Next: Thermostats and barostats
Up: Introduction: Molecular Dynamics
Previous: Introduction: Molecular Dynamics
Contents
The position of a set of particles q after a time step displacement 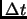 can be obtained by a Taylor expansion
can be obtained by a Taylor expansion
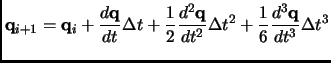 |
(2.101) |
where in the second term in the right-hand of equation 1.101 appears the velocity
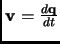 and in the
third term the acceleration
and in the
third term the acceleration
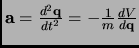
Developing the same expansion
at a previous step and added to equation 1.101, with both equations truncated at third order, give place to the
Verlet algorithm
which is the basis of the current molecular dynamics simulations techniques
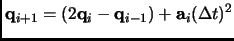 |
(2.102) |
The acceleration is taken from the derivatives of the potential energy and at the initialization point 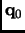 the previous
positions can be estimated as
the previous
positions can be estimated as
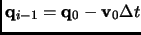 .
The Verlet algorithm offers several numerical problems.
In addition, the fact that the velocity does not appear explictly is a problem when generating ensembles at constant temperature.
.
The Verlet algorithm offers several numerical problems.
In addition, the fact that the velocity does not appear explictly is a problem when generating ensembles at constant temperature.
There are several improvements to the Verlet algorithm.
The Leap-Frog algorithm includes the velocity in its equations
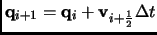 |
(2.103) |
where the velocity is
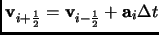 |
(2.104) |
velocity Verlet or the higher order predictor-corrector are other alternative integration methods.
Discussion about their adequacy, the numerical stability, the energy conservation and the time-reversible character must be
found in the extensive bibliography [15,50,13].




Next: Thermostats and barostats
Up: Introduction: Molecular Dynamics
Previous: Introduction: Molecular Dynamics
Contents
Xavier Prat Resina
2004-09-09