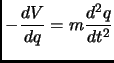Theoretical methods used in this thesis:
Molecular Dynamics Methods

Classical molecular dynamics (MD) can be used to propagate in time the nuclear coordinates of molecular system using the classical equations of motion^2.10

$$-\frac{dV}{dq}= m\frac{d^2q}{dt^2}$$ (2.100)

This is an excellent approximation for many particles, however, when we consider light particles such as hydrogen the quantum nature of the molecules must be considered [168] and we must recover the equations of nuclear quantum motions (section 1.2.1.3).

Equation 1.100 must be solved numerically propagating a trajectory at small time-steps. While a typical time-step is about one femtosecond (10$^{-15}$) most of chemical interesting events take place at time scales several orders of magnitude higher (micro or millisecond). Therefore the MD equations should be propagated until 10$^9$-10$^{12}$ steps to observe a reactive event (rare event). Despite of the recent acceleration techniques [169] this task is yet too expensive to be performed in the nowadays computers. This gap of time scales makes that so far Molecular Dynamics are rarely used to obtain a real picture of the thermically activated chemical processes. Therefore, in this thesis MD will be employed as a technique that may be used to compute equilibrium as well as kinetic properties of a many-body system. Most of these properties can also be computed with Monte Carlo (MC) techniques. Although MC covers a vast area of techniques they will not be commented here, and it may be found in the literature [13,15,50].

In this section, the main topics of molecular dynamics techniques are presented. However it must be taken in consideration that MD is a huge field of research and we will only mention those methods that we will apply to model our enzymatic system. In this sense, a volume of the Account of Chemical Research was dedicated to review the state of the art in Molecular Dynamics simulations of biomolecules [170].