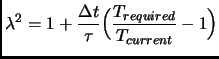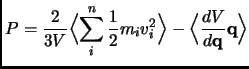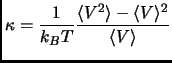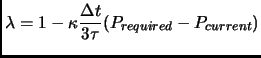Next: Constraints
Up: Introduction: Molecular Dynamics
Previous: Basic equations and algorithms
Contents
Using the equations of motion specified above the total energy is a constant of motion.
In this case the time averages obtained in this MD simulation are equivalent to ensemble
averages in microcanonical ensemble (NVE).
In order to run MD simulation at other non-NVE statistical ensembles we must introduce a
thermostat and/or barostat.
Constant Temperature:
The temperature of a particle system is related to the time average of the velocity of the particles
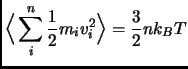 |
(2.105) |
The initial velocities can be given from a Maxwell-Boltzmann distribution at the desired temperature.
And the most intuitive strategy to keep constant the temperature would be to multiply at every step the
velocity of the particles by a scaling factor
 .
.
Other less rough approaches exist, Andersen introduced the stochastic collisions method[171] and
Berendsen and co-workers [172] introduced a
coupling parameter 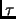 to an external bath
to an external bath
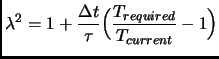 |
(2.106) |
However, the most popular strategy is the extended Lagrangian method that contains additional, artificial
coordinates and velocities. It was introduced by Andersen, Nosť[173] and reformulated by Hoover[174].
The reservoir is represented by an additional degree of freedom 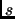 with a fictitious mass
with a fictitious mass 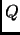 and with
potential energy
and with
potential energy
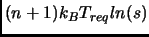 . The parameter
. The parameter 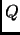 determines the coupling and the energy
flow between the reservoir and the real system and therefore the energy oscillations.
Some non-ergodicity problems have been reported with Nosť-Hoover method in this case a series of Nosť-Hoover chains are
introduced [175,176].
determines the coupling and the energy
flow between the reservoir and the real system and therefore the energy oscillations.
Some non-ergodicity problems have been reported with Nosť-Hoover method in this case a series of Nosť-Hoover chains are
introduced [175,176].
Constant Pressure:
A macroscopic system maintains constant pressure changing its volume.
The calculation of the pressure from a particle system is not as direct as the temperature (equation 1.105).
The Virial theorem can be used although it can give problems for Periodic Boundary systems.
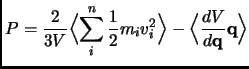 |
(2.107) |
The amount of volume fluctuation is related to the isothermal compressibility
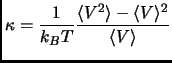 |
(2.108) |
Many of the methods used for the control of pressure are analogous to those used for the constant temperature.
The volume may be changed scaling the positions
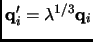 of the particles through a coupling parameter
of the particles through a coupling parameter 
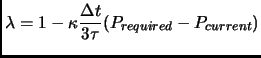 |
(2.109) |
Otherwise, the Nosť-Hoover scheme can be applied using an external piston as additional degree of
freedom [174,177].




Next: Constraints
Up: Introduction: Molecular Dynamics
Previous: Basic equations and algorithms
Contents
Xavier Prat Resina
2004-09-09
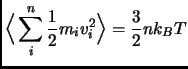
![]() to an external bath
to an external bath